前言
本学期中期的时候,出于个人兴趣,用unity自己做了两个小游戏:愤怒的小鸟和合成大西瓜。感觉非常有意思,完成度也还算可以,后续有空会分享一些制作过程和遇到的困难。在做那两个小游戏之前我是完全不了解整个游戏开发的流程的,也没有掌握相关的知识。感觉学校教的一些东西不太相关?由于个人还是想要向游戏行业发展(网安太难了感觉提不起兴趣来),所以觉得有必要来系统地学习一下在国内游戏领域应用十分广泛的计算机图形学(computer graphics)。
我是看的《Fundamentals of Computer Graphics》这本书,俗称虎书。在b站上看的闫令琪老师的课。
变换矩阵(Transformation Matrices)
变换矩阵是数学线性代数中的一个概念。在线性代数中,线性变换能够用矩阵表示。如果$T$是一个把$R_n$映射到$R_m$的线性变换,且$x$是一个具有$n$个元素的列向量 ,那么我们把$m×n$的矩阵$A$,称为$T$的变换矩阵。
这是百科对变换矩阵的解释。而在图形学中,变换矩阵的作用十分之大,一切物体的缩放,旋转,位移等操作都可以通过变换矩阵作用得到。本文将会介绍一些常用的变换矩阵。
前置知识
学习之前我们需要掌握一些线性代数的知识,学过这门课的应该都感觉不难,是最基础的一些知识。遥想当年我线代期末考了满分
向量加减
点乘积、叉乘积、右手螺旋定则
矩阵乘法
2D线性变换
既然由上边的定义了解到变换矩阵是通过乘法来体现的,我们就先来复习一下简单的矩阵乘法,接下来的运算都是此基础上的变式。在此式中$\begin{bmatrix} a_1 & a_2\ a_3 & a_4\ \end{bmatrix}$即为变换矩阵。
$$
\begin{bmatrix} a_1 & a_2\ a_3 & a_4 \end{bmatrix} \begin{bmatrix} x\ y \end{bmatrix} = \begin{bmatrix} a_1x+a_2y \ a_3x+a_4y \end{bmatrix}
$$
缩放(Scale)
缩放就是将物体沿着坐标轴进行压缩或拉伸的操作,它的变换矩阵定义如下
$$
scale(s_x,s_y)=\begin{bmatrix} s_x & 0\ 0 & s_y\end{bmatrix}
$$
所以,原来的矩阵与它相乘后变成了这样
$$
\begin{bmatrix} s_x & 0\ 0 & s_y\end{bmatrix} \begin{bmatrix} x\ y\end{bmatrix} = \begin{bmatrix} s_xx \ s_yy\end{bmatrix}
$$
即除了$(0,0)^T$点不动外,其他点都变成了$(s_xx,s_yy)^T$。即沿着坐标轴按照比例进行了缩放。看两个例子:
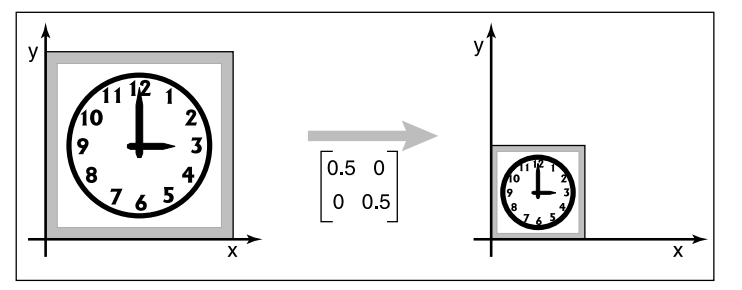
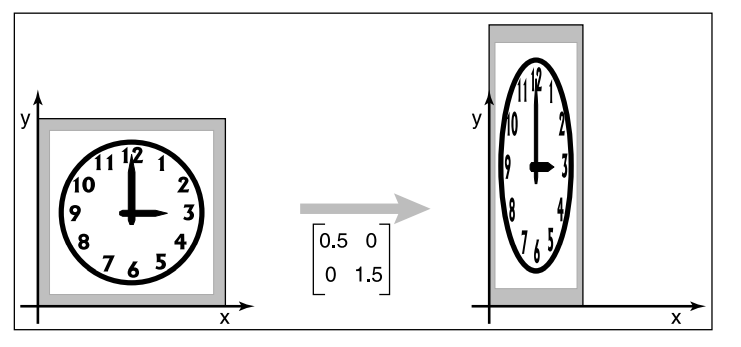
切变(Shearing)
切变直观理解就是把物体一边固定,然后拉另外一边。定义以及解释可能都有点抽象,结合图来分析:
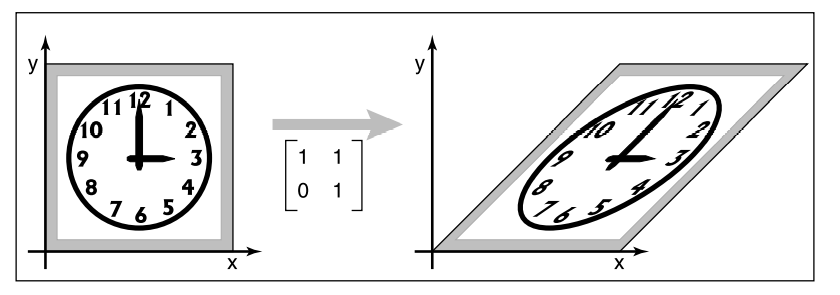
先不用管图中的变换矩阵,根据前面缩放的经验,我们只需找出点与点之间的数量关系即可。由图中可以看出,此变换在$y$轴上并没有做出任何改动,是$x$轴有向右拉伸的意思。再细看发现底端$y=0$这条也没有经过任何变换,看最上端这条直线变化最大(我们假设此时$y=1$,并向右移动了距离$a$),而原本位于$(0,1)$的这个点,变为了$(a,1)$。再看看中点呢?不难发现,原本位于$(0,\frac{1}{2})$的这个点,变为了$(\frac{a}{2},\frac{1}{2})$。所以在此图中,可以得到其变换矩阵为:
$$
shear=\begin{bmatrix} 1 & a\ 0 & 1\end{bmatrix}
$$
所以,原来的矩阵与它相乘后变成了这样
$$
\begin{bmatrix} 1 & a\ 0 & 1\end{bmatrix} \begin{bmatrix} x\ y\end{bmatrix} = \begin{bmatrix} x+ay \ y\end{bmatrix}
$$
推广到一般形式,我们可以得到切变的变换矩阵,其中$s=tan\phi$,$\phi$为坐标轴与拉伸边的夹角。这边解释一下,对应上图,$\phi$就是$y$轴和左边边的夹角,为啥上面的$tan\phi=a$,这个学过三角函数应该都知道。
$$
shear-x(s)=\begin{bmatrix} 1 & s\ 0 & 1\end{bmatrix} \quad\quad
shear-y(s)=\begin{bmatrix} 1 & 0\ s & 1\end{bmatrix}
$$
特别的,当$\phi=45°$时,$tan\phi=1$。
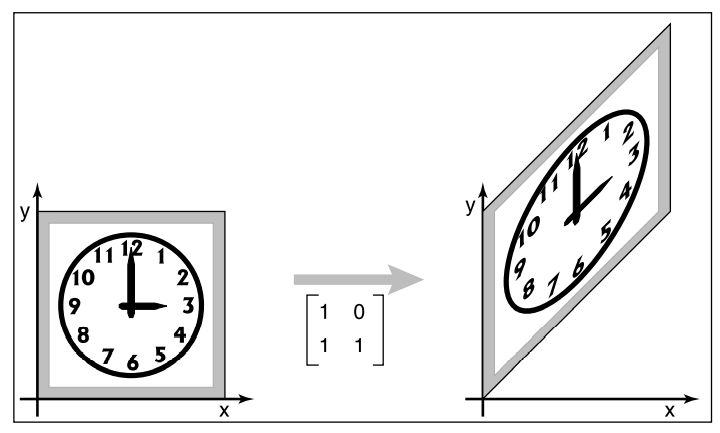
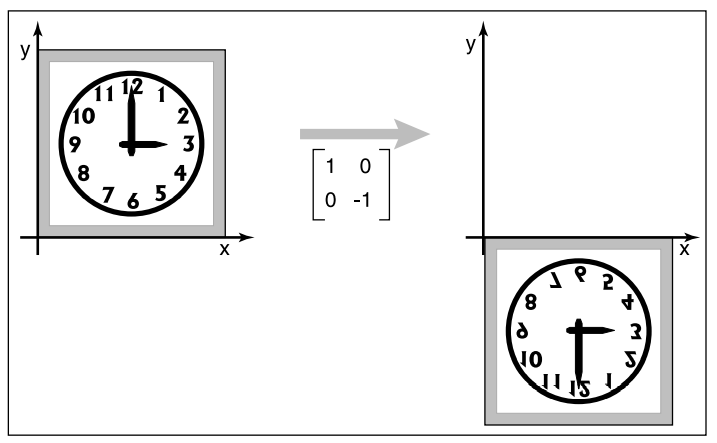
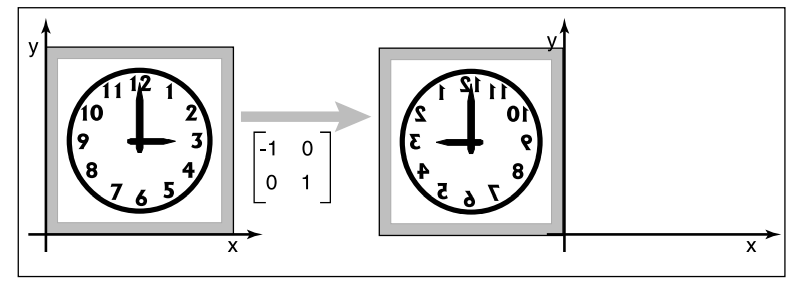
反射/对称(Reflection)
这个就没啥好说的了,就是镜面对称的意思。它的变换矩阵定义如下
$$
reflect-x=\begin{bmatrix} 1 & 0\ 0 & -1\end{bmatrix} \quad\quad
reflect-y=\begin{bmatrix} -1 & 0\ 0 & 1\end{bmatrix}
$$
所以,原来的矩阵与它相乘后变成了这样,以$x$轴的为例
$$
\begin{bmatrix} 1 & 0\ 0 & -1\end{bmatrix} \begin{bmatrix} x\ y\end{bmatrix} = \begin{bmatrix} x \ -y\end{bmatrix}
$$
旋转(Rotation)
旋转就是物体的转动了,先看一下它的变换矩阵
$$
rotate(\phi)=\begin{bmatrix} cos\phi & -sin\phi\ sin\phi & cos\phi\end{bmatrix}
$$
呃呃,乍一看很难理解,但我们还是只要弄清它的坐标变换就可以了,贴一张我自己画的分析图,应该还是挺清晰易懂的吧
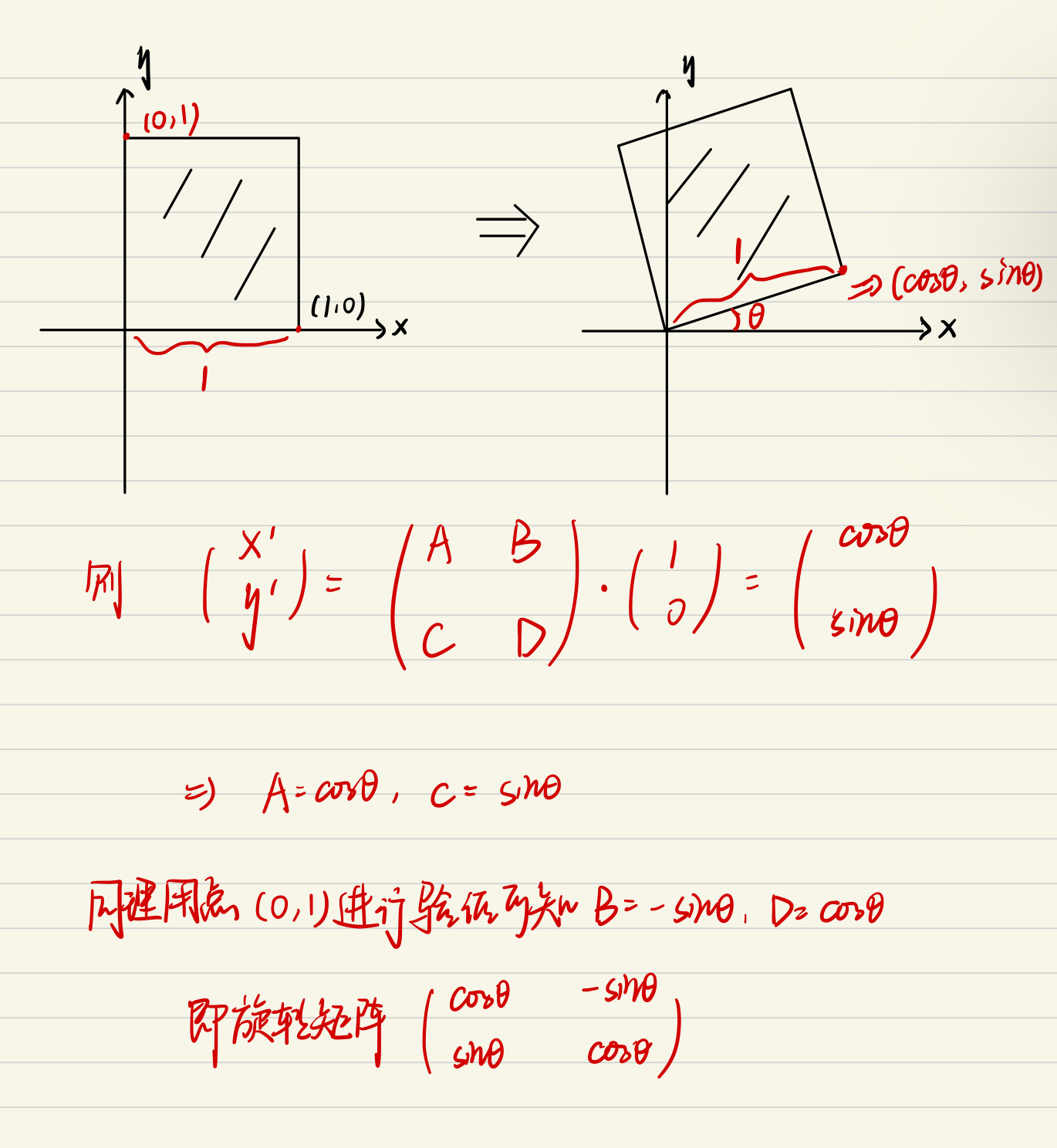
所以,原来的矩阵与它相乘后变成了这样
$$
\begin{bmatrix} cos\phi & -sin\phi\ sin\phi & cos\phi\end{bmatrix} \begin{bmatrix} x\ y\end{bmatrix} = \begin{bmatrix} xcos\phi-ysin\phi\ xsin\phi+ycos\phi\end{bmatrix}
$$
这是旋转$45°$的示例图:
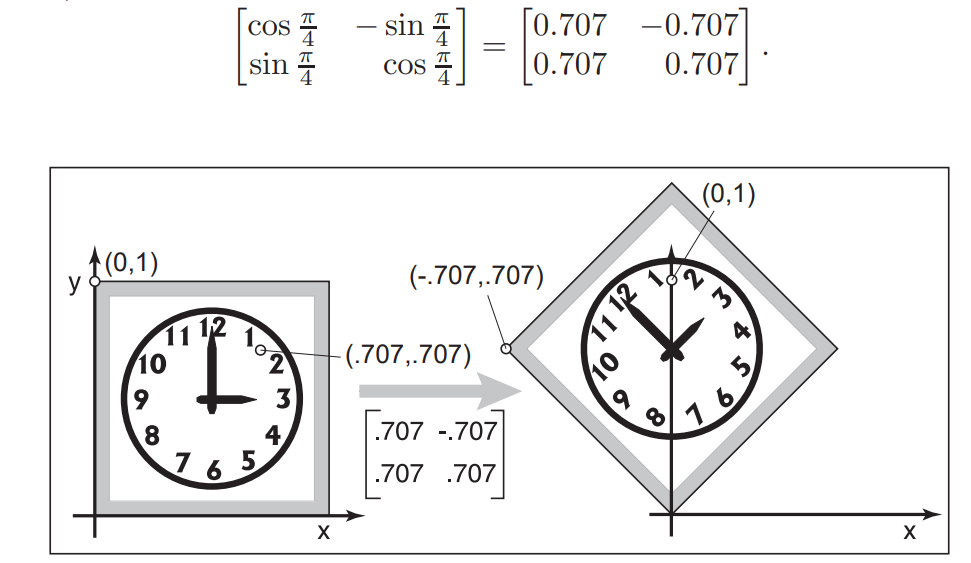
补充:由上述可以得到
$$
rotate(-\phi)=\begin{bmatrix} cos\phi & sin\phi\ -sin\phi & cos\phi \end{bmatrix}
$$
可以发现,$-\phi$的变换矩阵是$\phi$的变换矩阵的转置,也是$\phi$的变换矩阵的逆矩阵。所以,$-\phi$的变换矩阵的正交矩阵。
平移和仿射变换
对于一下的举例以及分析,都是针对二维变换。理解之后三维变换也就水到渠成,有类似特征。
平移(Translation)
我们都希望所有的物体位置变换都能够通过变换矩阵与向量的乘积一次性得到,但是偏偏有这个异类,就是平移。
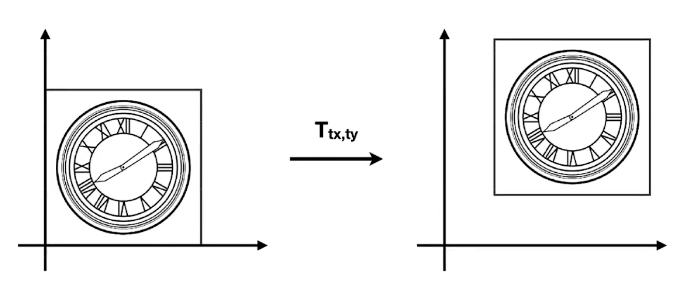
如上图,我们想要将图片右移$t_x$上移$t_y$,可得有方程组
$$
\begin{cases} x’=x+t_x\ y’=y+t_y\end{cases}
$$
怎么样的矩阵变换可以得到呢?
$$
\begin{bmatrix} x’\ y’\end{bmatrix} = \begin{bmatrix} a & b \ c&d\end{bmatrix} \begin{bmatrix} x \ y\end{bmatrix}+ \begin{bmatrix} t_x \ t_y\end{bmatrix}
$$
上述$a=d=1,b=c=0$。可以看到必须通过一个相加的操作才能得到正确的坐标变换表示,这破坏了我们的期望:结果用一个变换矩阵乘法得到。或者说,破坏了人们的懒惰性,但是啊人总是贪婪的,于是想着法子偷懒。还真就发明出来一个很有用很简洁的表示方法。就是齐次坐标。
齐次坐标(Homogeneous coordinates)
齐次坐标就是将一个原本是$n$维的向量用一个$n+1$维向量来表示,是指一个用于投影几何里的坐标系统,如同用于欧氏几何里的笛卡儿坐标一般。关于它的重要性:
《计算机图形学(OpenGL版)》的作者F.S. Hill Jr.曾说过一句话:
“齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换。”
于是我们知道,其重要性,主要有二,其一是区分向量和点,其二是易于进行仿射变化(Affine Transformation) 。
具体怎么应用呢?可以浅显的理解为:对于点来说,扩展为$(x,y,1)^T$。对向量来说,扩展为$(x,y,0)^T$
对于平移来说,就可以这样表示:
$$
\begin{bmatrix} x’\ y’\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 &t_x \ 0&1&t_y\ 0&0&1\end{bmatrix}\begin{bmatrix} x \ y\ 1\end{bmatrix}= \begin{bmatrix} x+t_x \ y+t_y\ 1 \end{bmatrix}
$$
这样就成功的表示为了乘积的形式,而增加的维度并不会对程序效率等造成很大影响,是一个很棒的解决方案。此时变换矩阵和齐次坐标分别为:
$$
\begin{bmatrix} 1 & 0 &t_x \ 0&1&t_y\ 0&0&1 \end{bmatrix} \quad\quad\quad\quad\quad
\begin{bmatrix} x \ y\ 1\end{bmatrix}
$$
上述,如果点被拓展为扩展为$(x,y,w)^T$,那么$x$、$y$就要变为$\frac{x}{w}$、$\frac{y}{w}$来表示。
这是针对每个点的平移来说的,那么为什么向量要拓展为$(x,y,0)^T$,最后是一个零呢?
$$
\begin{bmatrix} x’\ y’\ 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 &t_x \ 0&1&t_y\ 0&0&1 \end{bmatrix} \begin{bmatrix} x \ y\ 0 \end{bmatrix}= \begin{bmatrix} x \ y\ 0 \end{bmatrix}
$$
套用上面的公式,我们得到了上述结果。我们知道向量只跟两个要素有关,长度和方向,所以移动的$t_x$,$t_y$不应对此产生影响,故拓展为$(x,y,0)^T$,刚好解决了此问题。
仿射变换(Affine Transformation)
再看上面那个名人名言中的:齐次坐标有利于进行仿射变换。那么仿射变换又是什么呢?
个人理解仿射变换其实是就是上述两种简单变换的叠加:一个是线性变换,一个是平移变换
仿射变换变化包括缩放、旋转、反射、错切以及平移,原来的直线仿射变换后还是直线,原来的平行线经过仿射变换之后还是平行线,这就是仿射。就是我们上述介绍的变换的组合。当然也就是我们介绍齐次坐标所用到的矩阵变化。
一个集合的仿射变换为:
$$
f(x)=Ax+b,x\in X
$$
仿射变换是二维平面中一种重要的变换,在图像图形领域有广泛的应用,在二维图像变换中,一般表达为:
$$
\begin{bmatrix} x’\ y’\ 1 \end{bmatrix} = \begin{bmatrix} R_0 & R_1 &t_x \ R_2&R_3&t_y\ 0&0&1 \end{bmatrix} \begin{bmatrix} x \ y\ 1 \end{bmatrix}
$$
针对二维,它的变化是有规律的。比如最后一行是固定的$(0,0,1)$,而第一、二行前两列是要进行的线性变换,而最后一列是要平移的距离$t_x$,$t_y$。
平移变换矩阵
据此可以得出引入齐次坐标后仿射变化的变换矩阵了,对于平移:
$$
M=\begin{bmatrix} 1 & 0 &t_x \ 0&1&t_y\ 0&0&1 \end{bmatrix}
$$
缩放、切变、反射、旋转变换矩阵
同理,对于线性变换的四种,由于没有平移量,故$t_x$,$t_y$都为0,所以它们的变换矩阵:
$$
M=\begin{bmatrix} A & B &0 \ C&D&0\ 0&0&1 \end{bmatrix}
$$
具体A、B、C、D的内容参照上面的线性变化。
变换的组合与分解(Combination and decomposition of transformations)
组合
变换的组合其实就是上述线性与平移变换的叠加变换。需要注意的是变换的顺序:先线性后平移。
看下面一个例子,如果进行图示的变换呢?
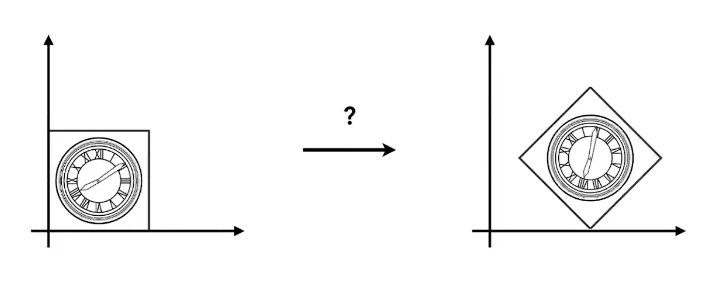
第一种方案是先平移后旋转,显然是不行的。
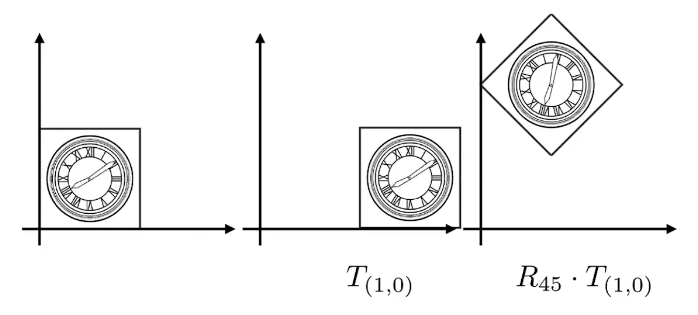
先旋转后平移是可以的。
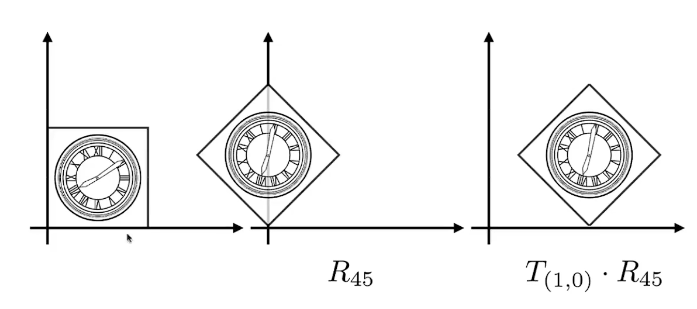
为什么一定要保持这个顺序呢?因为矩阵乘法没有交换律!
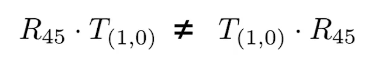
而针对数学表达来说,我个人形象的理解为遵循就近原则,向量先与最接近的变换矩阵相乘。
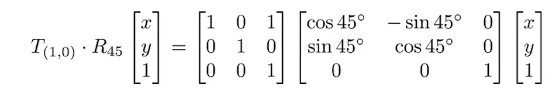
分解
分解其实就是组合的逆过程,一种简单的方法是:先将左下点移动到原点之后再进行线性与平移操作。
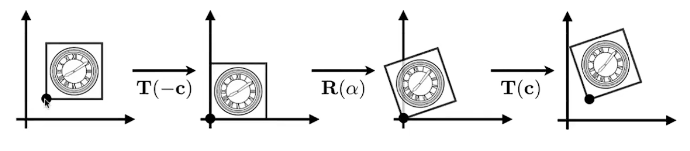
3D变换
3D变换跟上述的2D变化大多拥有相同的规律,无论是考不考虑齐次坐标,也就相当于多增加了一个维度。
仿射变换在三维当中的应用表达式为:
$$
\begin{bmatrix} x’\ y’\ z’ \1 \end{bmatrix} = \begin{bmatrix} R_0 & R_1 & R_2&t_x \ R_3&R_4&R_5&t_y\ R_6&R_7&R_8&t_z\ 0&0&0&1 \end{bmatrix} \begin{bmatrix} x \ y\z \1 \end{bmatrix}
$$
同样地,如果点被拓展为扩展为$(x,y,z,w)^T$,那么$x$、$y$、$z$就要变为$\frac{x}{w}$、$\frac{y}{w}$、$\frac{z}{w}$来表示。
平移变换矩阵
3D变换的平移用齐次坐标表示的变换矩阵为:
$$
translation(t_x,t_y,t_z)=\begin{bmatrix} 1 & 0 &0&t_x \ 0 & 1 &0&t_y\ 0 & 0 &1&t_z \ 0 & 0 &0&1 \end{bmatrix}
$$
缩放变换矩阵
3D变换的缩放用齐次坐标表示的变换矩阵为:
$$
scale(s_x,s_y,s_z)=\begin{bmatrix} s_x & 0 &0&0 \ 0 & s_y &0&0\ 0 & 0 &s_z&0 \ 0 & 0 &0&1 \end{bmatrix}
$$
还有切变与反射这边就不展开了,都是类似的
旋转变换矩阵
绕坐标轴旋转
3D当中的旋转可以说是最难的一种物体变换,和2D有很大的不同。首先考虑最简单的绕三个轴旋转,变换矩阵依次为:
$$
R_x(\alpha)=\begin{bmatrix} 1 & 0 &0&0 \ 0 & cos\alpha &-sin\alpha&0\ 0 & sin\alpha &cos\alpha&0 \ 0 & 0 &0&1 \end{bmatrix} \quad\quad
R_y(\alpha)=\begin{bmatrix} cos\alpha & 0 &sin\alpha&0 \ 0 & 1 &0&0\ -sin\alpha & 0 &cos\alpha&0 \ 0 & 0 &0&1 \end{bmatrix} \quad\quad
R_z(\alpha)=\begin{bmatrix} cos\alpha & -sin\alpha &0&0 \ sin\alpha & cos\alpha &0&0\ 0 & 0 &1&0 \ 0 & 0 &0&1 \end{bmatrix}
$$
我们所采用的是右手系,因此旋转是有定向的。正如在二维,是$x$轴向$y$轴旋转。类似地,运用右手螺旋定则,对应到3维便是绕$z$轴旋转($x$轴转向$y$轴),不难推出绕$x$轴旋转($y$转向$z$),绕$y$轴旋转($z$转向$x$),就是这么一个规律$$ x->y->z->x…$$这样就可以将问题简化为固定一边不变,而另外两个维度就是2D变换的变换矩阵。
因此理解了上面这个来看绕$x$(绕$x$轴,故$x$不变,且$y$转向$z$)和$z$(绕$z$轴,故$z$不变,且$x$转向$y$)旋转的变换矩阵。那绕$y$轴为啥会有所不同呢?主要原因是我们是固定$y$轴,然后由且$z$转向$x$,而不是$x$转向$z$,故有所不同。
同上述2D,3D变换中的旋转矩阵也都是正交矩阵
绕任意轴旋转
之前2D中变换的分解我们可以了解到这么一个思想:先把物体平移到原点,再进行线性变化,之后将物体平移回去。在3D旋转中我们同样可以借鉴这个思想,我们可以先将物体整个平移到相较于它的坐标轴零点,然后进行相应的旋转,之后再把物体平移回去即可。